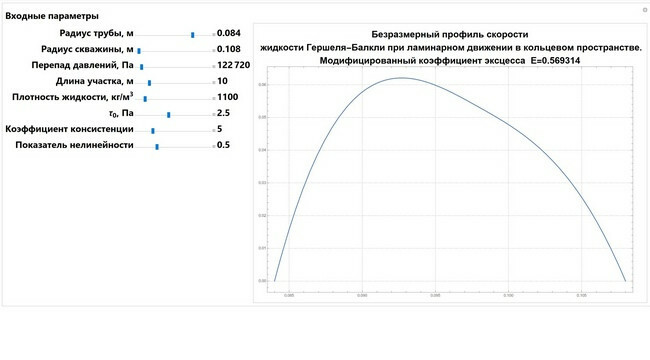
Применение буровых промывочных жидкостей необходимо при бурении нефтяных скважин. Эти жидкости обеспечивают безопасное и безаварийное ведение буровых работ. Так как буровые промывочные жидкости обладают псевдопластичными свойствами, то есть имеют тенденцию к уменьшению вязкости при их движении, то технологам нужно с особым вниманием подходить к разработке их рецептуры. Задача эта очень непростая, требующая комплексного подхода к изучению. Доцент кафедры «Бурение нефтяных и газовых скважин» Политеха Василий Никитин выяснил, что реологическая модель жидкости Гершеля – Балкли позволяет наиболее точно описывать реальные параметры бурового раствора, а ее использование при решении дифференциального уравнения движения жидкости приводит к новым научно-практическим результатам.
– Многие технологические параметры процесса бурения скважины рассчитываются, исходя из выбора реологической модели буровой промывочной жидкости. Например, это касается индекса очистки скважины на основании скорости восходящего потока. Проблема в том, что потоки жидкостей разных реологических классификаций обладают значительными различиями в распределении скоростей в восходящем потоке, – поясняет Василий Никитин.
Так, Ньютоновская модель недопустима при моделировании реологических свойств буровых систем, так как не учитывает начальных напряжений сдвига и возможность изменения вязкости при движении. Реологическое уравнение Шведова – Бингама не берет в расчет изменение вязкости при изменении скорости сдвига. Степенная модель Оствальда – де Ваале учитывает изменение вязкости, но не предусматривает начальных напряжений сдвига.
– Так как современные промывочные жидкости имеют начальное напряжение сдвига и тенденцию к изменению вязкости при изменении скорости сдвига, то возникает необходимость использования трехпараметрического реологического уравнения Гершеля – Балкли, учитывающего оба признака неньютоновской среды. Научная новизна заключается в нахождении численного решения стационарного модифицированного дифференциального уравнения движения Навье – Стокса для жидкости Гершеля – Балкли и введения нового критериального параметра качества очистки ствола скважины, – рассказывает о своем научном открытии ученый Политеха.
Представленная стационарная одномерная модель движения жидкости Гершеля – Балкли не реализует все стороны физического поведения течения неньютоновской жидкости в кольцевом пространстве, но может показывать определенную тенденцию. Это позволяет моделировать движение буровых промывочных жидкостей с некоторыми допущениями.
Значимость исследования подкрепляется серией численных экспериментов, проведенных с использованием уникального программного обеспечения, на которое Василий Никитин получил патент (№ 2022661194).
– Многие технологические параметры процесса бурения скважины рассчитываются, исходя из выбора реологической модели буровой промывочной жидкости. Например, это касается индекса очистки скважины на основании скорости восходящего потока. Проблема в том, что потоки жидкостей разных реологических классификаций обладают значительными различиями в распределении скоростей в восходящем потоке, – поясняет Василий Никитин.
Так, Ньютоновская модель недопустима при моделировании реологических свойств буровых систем, так как не учитывает начальных напряжений сдвига и возможность изменения вязкости при движении. Реологическое уравнение Шведова – Бингама не берет в расчет изменение вязкости при изменении скорости сдвига. Степенная модель Оствальда – де Ваале учитывает изменение вязкости, но не предусматривает начальных напряжений сдвига.
– Так как современные промывочные жидкости имеют начальное напряжение сдвига и тенденцию к изменению вязкости при изменении скорости сдвига, то возникает необходимость использования трехпараметрического реологического уравнения Гершеля – Балкли, учитывающего оба признака неньютоновской среды. Научная новизна заключается в нахождении численного решения стационарного модифицированного дифференциального уравнения движения Навье – Стокса для жидкости Гершеля – Балкли и введения нового критериального параметра качества очистки ствола скважины, – рассказывает о своем научном открытии ученый Политеха.
Представленная стационарная одномерная модель движения жидкости Гершеля – Балкли не реализует все стороны физического поведения течения неньютоновской жидкости в кольцевом пространстве, но может показывать определенную тенденцию. Это позволяет моделировать движение буровых промывочных жидкостей с некоторыми допущениями.
Значимость исследования подкрепляется серией численных экспериментов, проведенных с использованием уникального программного обеспечения, на которое Василий Никитин получил патент (№ 2022661194).